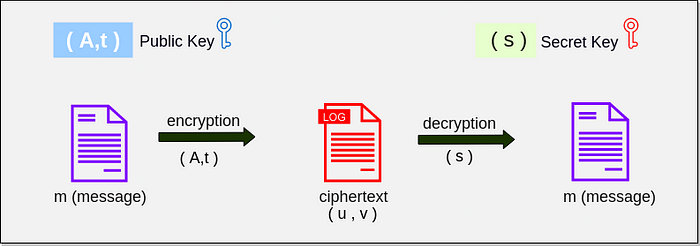
Learning with Errors: Quantum-Proof Algorithm

Author: Aditya Koranga

Published: June 27, 2022

Introduction

A foundational concept in lattice-based cryptography is the Learning with Errors (LWE) problem. LWE is a public key encryption method regarded as robust and is utilized by various lattice-based algorithms, including Kyber and Frodokem. As reflected by its name, the method incorporates the intentional addition of errors into its mathematical construction, which is critical for its security properties.

How LWE Works

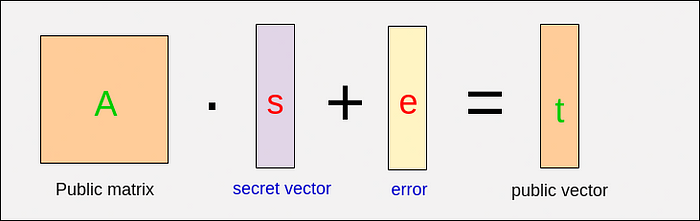
The basic framework begins with the following linear equation:

A . s = t

Where:

• A is a public matrix,

• s is a secret vector,

• t is a public vector.

Thus, (A, t) acts as the public key pair and s is the private key.

Given that both A and t are public, it is straightforward to determine the secret vector s using basic algebraic techniques such as Gaussian elimination. To address this, LWE introduces an additional error vector, making the equation:

A . s + e = t

Here, e is a small error (noise) vector. This single modification makes it computationally difficult to recover s from public information, thereby strengthening security.

With the inclusion of error e, the public key remains (A, t), while s continues as the private key. The process then moves to encryption and decryption.

Encryption

Consider a message m that needs to be encrypted (typically converted into a polynomial form). The encryption process utilizes the public key pair (A, t) and incorporates additional randomness:

• The ciphertext consists of two components:

  • u: a cipher polynomial,

  • v: a polynomial vector.

These are computed as follows, using error terms e1, e2, and e3:

v = t . e1 + e2 + m
u = A . e1 + e3

Note that error e1 is used in both equations. Once the ciphertext is generated, it can be transmitted securely.

Decryption

Decryption involves the use of the secret key s. The original message d is recovered using:

d = v — s . u

Substituting the values for v and u:

d = t . e1 + e2 + m — s . (A . e1 + e3)
d = t . e1 + e2 + m — A . s . e1 — s . e3

Given A . s + e = t, substituting for t:

d = (A . s + e) . e1 + e2 + m — A . s . e1 — s . e3
d = A . s . e1 + e . e1 + e2 + m — A . s . e1 — s . e3

Canceling terms:

d = e . e1 + e2 + m — s . e3
d = m + e . e1 + e2 — s . e3

The remaining terms (e . e1 + e2 — s . e3) are small noise values, which can be removed using mathematical rounding (commonly a q/2 method). After error correction, the original message m is recovered, thus completing the decryption.

Other Types of LWE

Variants of the LWE problem include Ring-LWE and Module-LWE (M-LWE). Kyber, for instance, utilizes M-LWE. These methods retain the core principles of standard LWE but differ in the construction of the public matrix A. In M-LWE, elements of one column may be repeated in other columns.

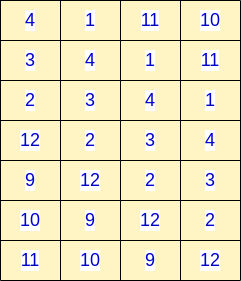
Public matrix in M-LWE

Complete Flow Diagram

The full process for the Learning with Errors method is illustrated below.